AVL Tree

Introduction of AVL Tree

• The AVL tree is named after its two Soviet Union inventors, Georgy Adelson-Velsky and Evgenii Landis, who published it in their paper “An algorithm for the organization of information” in 1962.
• The AVL tree is also called a Self-balancing BST.

Definition

• An AVL Tree is a special type of Binary Search Tree (BST) that keeps itself balanced at all times.
• An AVL tree is an automatic self-balancing binary search tree in which each node maintains extra information (called a balance factor)using the tree rotation technique.

Properties/Characteristics

• In this tree, the heights(h) of the two child subtrees of any node are either the same or differ by at most one. If at any time they differ by more than one, rebalancing is required and done using the concept of Balance Factor concept to restore the self-balanced property.
• All the nodes in this tree store their own balance factor value, either -1, 0, or +1.
• Rebalancing in this tree is done by Tree Rotation.
• If the height of the AVL tree is h, the maximum number of nodes can be 2^h+1 – 1.
• The minimum number of nodes(n) in this tree with height h can be N(h) = N(h-1) + N(h-2) + 1

• The height or depth of the AVL tree is O(log n).
• The insertion and Deletion time complexity in this tree is O(log n). 
• The searching time complexity of this tree is O(n).

• Balance Factor(bf) :

  • In an AVL tree, the balance factor is used to check whether the tree is balanced or not after every insertion or deletion of a node from the AVL tree.
  • The balance factor of a node is the difference between the height of its left subtree and the height of its right subtree.
  • The bf is calculated as, Balance Factor (bf) = Height of Left Subtree (hL) – Height of Right Subtree(hR).
  • The value of the balance factor (bf) of a node in a height-balanced/AVL tree may take on one of the values –1, 0, or +1. The tree is AVL and balanced.
    • If the balance factor = 0, it means the left and right subtrees are of equal height, i.e., a perfectly balanced AVL Tree.
    • If the balance factor = +1, it means the left subtree is taller by one level, and the AVL tree is still balanced.
    • If the balance factor = -1, it means the right subtree is taller by one level, and the AVL tree is still balanced.
  • If the balance factor < -1 or > +1, the node is unbalanced and the tree is not AVL, hence the AVL tree needs rotation to restore balance.

• Tree Rotation :

  • Tree rotations are techniques to restore balance when the tree becomes unbalanced.
  • Tree rotation is an operation performed on an AVL tree that changes the structure of the tree without interfering with the order of the elements.
  • A tree rotation moves one node up in the tree and one node down at a time.
  • It is used to change the shape of the tree for rebalancing, and in particular to decrease its height by moving smaller subtrees down and larger subtrees up.
  • Tree rotation operation improved the performance of tree operations such as searching, insertion, deletion, etc.
  • This tree applies the tree rotation operation automatically/dynamically.
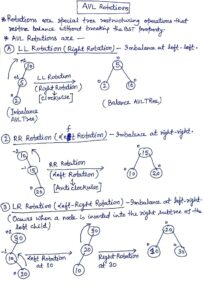
  • There are the following types of tree rotation –
    • LL Rotation
    • RR Rotation
    • LR Rotation
    • RL Rotation
    • Left-Left (LL) Rotation – This rotation occurs when a new node is inserted into the left subtree of the left child. It performs a Right Rotation.
    • Right-Right (RR) Rotation – This rotation occurs when a new node is inserted into the right subtree of the right child. It performs a Left Rotation.
    • Left-Right (LR) Rotation – This rotation occurs when a new node is inserted into the right subtree of the left child. It performs a Left Rotation on the child, then a Right Rotation on the parent.
    • Right-Left (RL) Rotation – This rotation occurs when a new node is inserted into the left subtree of the right child. It performs a Right Rotation on the child, then a Left Rotation on the parent.

Operations in an AVL tree

• Insertion
  • Insert the new node like in a normal BST.
  • After insertion, update the balance factor of each ancestor node, if required.
  • If the balance factor becomes unbalanced (greater than +1 or less than -1), perform rotation to restore balance.
  • Now the AVL tree becomes stable.
• Deletion
  • Delete the specified node, like in a normal BST.
  • Update the balance factor on the path back to the root, after deletion.
  • If an imbalance occurs, perform the required rotation.
• Searching
  • Same as a normal BST (compare value and go left or right).
  • But since the tree is balanced, searching is always efficient.

Advantages

• Efficient Searching – Since the tree is self-balanced, the maximum height is O(log n), so searching is very fast. In other words, it has a faster and better search time.
• Guaranteed Performance – Unlike a normal BST, which may degrade to O(n) in the worst case, AVL trees guarantee O(log n) performance for insertion, deletion, and searching.
• Keeps Data Sorted – In-order traversal of an AVL tree always gives data in ascending order.
• Useful in Real-Time Systems – Especially in applications where fast lookups and updates are critical.
• It is simple to implement.
• The structure or height of the AVL tree is always balanced.
• This tree gives better search time complexity than Binary Search trees.
• This tree has self-balancing capabilities.

Disadvantages

• Complexity in Insertion/Deletion – After each insertion or deletion, balance factors must be updated, and sometimes multiple rotations are required.
• Extra Storage – Each node must store its height or balance factor, which increases memory usage.
• Each node of this tree contains extra information as a balance factor.
• Tree rotation and self-balancing in this tree is are expensive operations.
• Insertion and deletion operations take comparatively more time to complete.

Use/Application

• Used extensively in database applications for indexing, for quick search and retrieval.
• Organizing files in a balanced way for faster access.
• Operating systems use AVL-like trees for managing free memory blocks in memory management.
• Network routers may use AVL trees to store routing information efficiently in their routing tables.