Binary Search Tree

Introduction of Binary Search Tree

• They are also called Ordered Binary Trees, as each node in a BST is placed according to a specific order.

Definition

• A binary search tree is a non-linear, non-cyclic data structure and is an extension/type of binary tree that may be empty or have at most two children at each node.
• A binary search tree is either empty or it contains a root node together with two binary search trees called the left subtree and the right subtree of the root.

Characteristics

• A BST is said to be perfectly balanced if for every internal node, there is are equal number of nodes in its left and right sub-trees.
• An unbalanced/one-sided/Degenerate Binary Search Tree is a BST in which all the elements are arranged on one side only, i.e., either the left or the right side only.
• Each node in the BST is itself a BST, i.e., the BST is naturally recursive in nature.

Properties

• In a BST:

  • Each node has a minimum of zero or at most two children – a left child and a right child.
  • Left Child Rule – The value of every node in the left subtree is smaller than the value of the parent node.
  • Right Child Rule – The value of every node in the right subtree is greater than the value of the parent node.
• Each node in a BST has <= 2 children.
• The left subtree of a node contains only nodes with keys less than the node’s key, i.e., all keys in the left subtree are smaller than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key, i.e., all keys in the right subtree are larger than the node’s key.
• The left and right subtrees each must also be a binary search tree.

Implementation/Representation of BST

• The node of a typical BST can be represented as –

Operation in BST

• There are some common operations usually seen in a typical BST. These are –
  • Creation of a new/fresh BST.
  • Traversing/Printing the node values in BST.
  • Insertion of a new node in the existing BST.
  • Deletion of one/more nodes from an existing BST.
  • Finding/Searching a specific node value from an existing BST.

Algorithm for Insertion of the new/fresh node in an existing BST:-

• • Start from the root.
  • Compare the new value with the current parent node:
    • If the value is smaller → go to the left subtree and insert the new value on an empty spot (NULL) is found.
    • If the value is larger → go to the right subtree and insert the new value on an empty spot (NULL) is found.

Algorithm for Searching for the specific value in an existing BST:-

• • Start from the root.
  • Compare the target/searched value with the current node value:
    • If value is equal → value found.
    • If the value is smaller → searching starts in the left subtree and continues until a value is found or NULL is reached (not found).
    • If the value is larger → searching starts in the right subtree and continues until a value is found or NULL is reached (not found).

Algorithm for Deletion of the node from an existing BST:-

• • A binary search tree (BST) is a binary tree data structure where each node has at most two children, and the values in the left subtree of a node are less than or equal to the node’s value, while the values in the right subtree are greater than the node’s value.
  • Deleting a node from a BST involves maintaining the property of a BST while removing the desired node.
  • The step-by-step algorithm for deleting a node from a BST is as follows:

Step 1: Start at the root of the tree.

Step 2: Search for the node to delete:

• • • • If the node to delete has a value less than the current node’s value, move to the left subtree.
      • If the node to delete has a value greater than the current node’s value, go to the right subtree.
      • If the current node’s value is equal to the value of the node to delete, we have found the node to delete.

Step 3: Once we have found the node to delete, there are three conditions/cases to consider:

a. Node having no children (leaf/terminal node):

• • • • Remove the node from the tree.

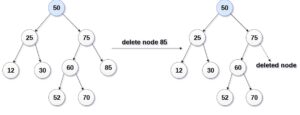
b. Node with one child, either left or right:

• • • • Replace the root node to delete with its only child. If it has the left child, replace it with the left child value; if it has the right child, replace it with the right child value.

c. Node with two children:

• • • • When the node with two children is deleted, its place is filled with either the left subtree’s (the largest node) value or the right subtree’s (the smallest)value, and re-adjusted using the BST rule.

Traversal/Printing in BST

• Traversal is a visit to every node in the BST, and performing some specific operation on it to get the stored values.
• There are 4 common types of traversals in a BST. These are –

(a) Pre-Order Traversal: The order of traversal in pre-order traversal is-

1. Visit the root node first.
2. Now, traverse its left (associated) subtree.
3. Then, traverse its right (associated) subtree

(b) In-Order Traversal: The order of traversal in In-order traversal is-

(c) Post-Order Traversal: The order of traversal in post-order traversal is-

(d) Level-Order Traversal: 

• Here, each node of the BST is traversed level by level (top to bottom) in order of its appearance/location.
• In each level, traversing order is from left to right.

Advantages

• Efficient Searching – A Binary Search Tree allows searching for an element very efficiently, and if the tree is balanced, the search operation can be performed in approximately logarithmic time, that is, O(log n). Also, searching is very effective and becomes very easy due to the arrangement of data one-sided, i.e., smaller than the root is on the left side and higher on the right side.
• Sorted Data – Performing an in-order traversal of a Binary Search Tree naturally produces the data elements in sorted order without needing any additional sorting algorithm.
• Dynamic Structure – A Binary Search Tree can easily grow or shrink in size as elements are inserted or deleted, making it flexible and suitable for applications where the amount of data changes frequently.
• BST has an efficient & effective working when compared to arrays and linked lists.
• Insertion and deletion operations are comparatively faster than other data structures like linked lists and arrays.

Disadvantages

• If the BST becomes unbalanced/one sided, operations may degrade to O(n), i.e., an imbalanced or degenerated form of BST has less usability and is more complex.
• Requires additional memory for pointers (left and right references).

Use/Applications

• Databases – Binary Search Trees are widely used in databases for multilevel indexing to handle a large no. of data items, which allows quick lookups and efficient retrieval of stored records.
• Search Engines – Search engines make use of Binary Search Trees to store dictionary words in a structured way so that searches and suggestions can be performed faster.
• File Systems – In file systems, Binary Search Trees help in organizing hierarchical data such as directories and files, making access and navigation easier.
• Dynamic Sorting – Binary Search Trees are useful in situations where data must be kept in sorted form at all times, since an in-order traversal of the tree automatically produces the elements in ascending order.
• BST is also used in applications that require a sorted list as input, such as online stores.
• BST is used to implement the Huffman coding algorithm.
• BSTs are also used to evaluate the expression by constructing expression trees.
• BST is also used in the construction of a digital dictionary.
• BST can also be used to implement various efficient searching algorithms.