Table of Contents
hide
Links for Complexity and its Type
- Complexity notations are mathematical ways that are used to express the growth rate of an algorithm’s time or space requirements (ignoring constants and lower-order terms) as the input size grows or becomes very large.
- Complexity notations actually describe algorithm efficiency.
Asymptotic Notations (n→∞):
- In computer science, complexity is expressed using asymptotic notations.
- Asymptotic notations are used to express the running time of an algorithm in terms of a function, whose domain is the set of natural numbers N={1,2,3,…..}. Such notations are convenient for describing the worst-case running time function T(n).
- Asymptotic notation gives the rate of growth, i.e., performance, of the run time for ‘sufficiently large input sizes’ (n→∞) and is not a measure of the particular run time for a specific input size.
- We generally want to find either or both an asymptotic lower bound and upper bound for the growth of our function. The lower bound represents the best-case growth of the algorithm, while the upper bound represents the worst-case growth of the algorithm.
- Asymptotic notations represent the limiting behaviour concerned with the increase in running time of an algorithm with the size of the input as a limit.
- The complexity function can also be used to compare two algorithms, P and Q, that perform the same task.
- Why Asymptotic Notations are Used
- To analyze algorithm performance independently of hardware.
- To compare algorithms for large inputs.
- To focus on growth behavior, not exact running time.
- There are three types of asymptotic notations: –
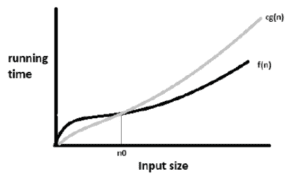
1. Big-Oh Notation(O)[Upper Bound/Worst Case]:
-
- This notation is used to express the Upper bound (maximum steps) required to solve a problem.
- O-notation is used to express the Upper bound (worst case) on a function.
- Suppose f(n) and g(n) are positive integers. This notation can be represented as: –
f(n) = O(g(n))
here, f(n)<cg(n) where n>=n0
-
- Here, f grows no faster than g.
- If there exist two positive constants c and n0 such that f(n) <= cg(n), i.e., f(n) is asymptotically less than or equal to g(n) for all values of n >=n0, where Big-O represents an upper bound.
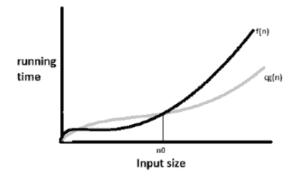
2. Big Omega Notation(Ω) [Lower Bound/Best Case]:
-
- This notation is used to express the Lower bound, i.e., the minimum (at least) steps required to solve a problem.
- Ω-notation is used to express the Lower bound (Best case) on a function.
- Suppose f(n) and g(n) are positive integers. This notation can be represented as: –
f(n) = Ω(g(n))
here, f(n)>=cg(n) where n>=n0
-
- Here,”f grows at least as fast as g”.
- If there exist two positive constants c and n0 such that f(n)>=cg(n), i.e., f(n) is asymptotically greater than or equal to g(n) for all values of n>=n0, where Ω represents a lower bound.
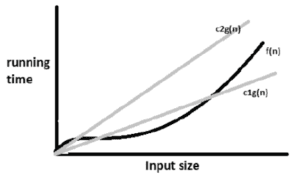
3. Big Theta Notation(θ) [Tight Bound/Average Case]:
-
- This notation is used to express both Upper & Lower bounds (also called a tight bound) to solve a problem.
- This Notation is used to express both upper and lower bounds (i.e., Average case) on a function.
- Suppose f(n) and g(n) are positive integers. This notation can be represented as: –
f(n)=θ(g(n))
here f(n)>=cg(n) where n>=n0
-
- Here, f(n) is a Big Theta of g(n).
- Here, “f grows exactly as fast as g” (i.e., sandwiched between multiples of g)
- If f(n) is Big O of g(n) and f(n) is Big Omega of g(n), i.e., c’g(n)<=f(n)<=c”g(n), i.e., f(n) is asymptotically equal to g(n) for all values of n>=n0 where θ represents exact bound.
4. Little Oh Notation(o) [Strict Upper Bound/Strict Worst Case]:
-
- It represents a strict upper bound.
- Here, the growth is slower than the given function.
5. Little Omega Notation(ω) [Strict Lower Bound/Strict Best Case]:
-
- It represents a strict lower bound.
- Here, the growth is faster than the given function.
Recurrence
- A recurrence relation is a mathematical equation that expresses the running time of a recursive algorithm in terms of smaller input sizes.
- It is mainly used to analyze recursive algorithms.
- It gives a solution using different methods of recurrence, which are as follows:
- Substitution method
- Recursion tree
- Master Theorem
![]()
0 Comments