(A) Asymptotic Notations (n→∞):
- Asymptotic notations are used to express the running time of an algorithm in terms of function, whose domain is the set of natural numbers N={1,2,3,…..}. Such notations are convenient for describing the worst case running time function T(n).
- Asymptotic notation gives the rate of growth, i.e. performance, of the run time for ‘sufficiently large input sizes’ (n→∞) and is not a measure of the particular run time for a specific input size.
- We generally want to find either or both an asymptotic lower bound and upper bound for the growth of our function. The lower bound represents the best case growth of the algorithm while the upper bound represents the worst case growth of the algorithm.
- Asymptotic notations represent the limiting behaviour concerned with the increase in running time of algorithm with size of input as a limit.
- The complexity function can be also be used to compare two algorithms P and Q that perform the same task.
- There are three types of asymptotic notations: –
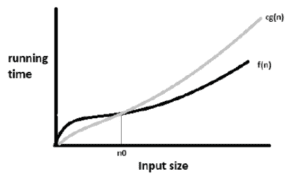
1. Big-Oh Notation(O):
-
- This notation is used to express Upper bound (maximum steps) required to solve a problem.
- O-notation is used to express the Upper bound (worst case) on a function.
- Suppose f(n) and g(n) be positive integers. This notation can be represented as: –
f(n) = O(g(n))
here, f(n)<cg(n) where n>=n0
-
- If there exists two positive constants c and n0 such that f(n) <= cg(n), i.e., f(n) is asymptotically less than or equal to g(n) for all values of n >=n0 where Big-O represents upper bound.
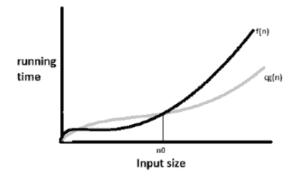
2. Big Omega Notation(Ω):
-
- This notation is used to express Lower bound i.e. minimum (at least) steps required to solve a problem.
- Ω-notation is used to express the Lower bound (Best case) on a function.
- Suppose f(n) and g(n) be positive integers. This notation can be represented as: –
f(n) = Ω(g(n))
here, f(n)>=cg(n) where n>=n0
-
- If there exists two positive constants c and n0 such that f(n)>=cg(n), i.e., f(n) is asymptotically greater than or equal to g(n) for all values of n>=n0 where Ω represents lower bound.
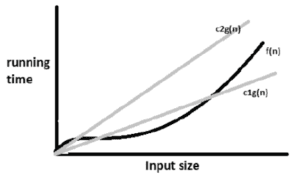
3. Theta Notation(θ):
-
- This notation is used to express both Upper & Lower bound, (also called tight bound) to solve a problem.
- This Notation is used to express both upper and lower bound (i.e. Average case) on a function.
- Suppose f(n) and g(n) be positive integers. This notation can be represented as: –
f(n)=θ(g(n))
here f(n)>=cg(n) where n>=n0
-
- Here, f(n) is a Big Theta of g(n).
-
- If f(n) is Big O of g(n) and f(n) is Big Omega of g(n), i.e., c’g(n)<=f(n)<=c”g(n), i.e., f(n) is asymptotically equal to g(n) for all values of n>=n0 where θ represents exact bound.
![]()
0 Comments