Introduction
- Adder is a very good example of Combinational Logic Circuits.
Definition
- An adder is a fundamental component in digital electronics devices and is used to perform arithmetic operations, specifically addition.
Characteristics
- Adders are found in the ALU of the CPU.
- Adders do not have their memory.
- Their output depends solely on the current inputs.
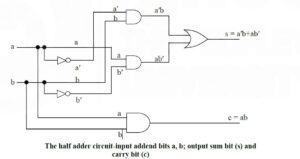
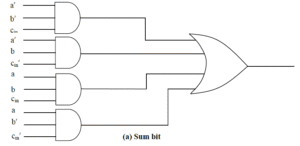
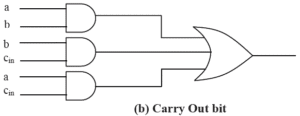
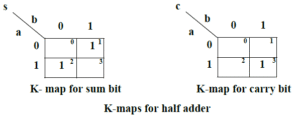
Types of Adder
(I) Half Adder
- This adder adds two single-bit binary numbers only(say a and b).
- This adder results in two output forms – Sum (s) and Carry-out (c).
Truth Table:
| a | b | Sum (s) | Carry-out (c) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Logic Equations:
- Sum (s) = a ⊕ b (XOR gate)
- Carry-out (c) = a ⋅ b (AND gate)
Circuit Diagram:
Thus, the Boolean expressions for them from the k-maps are:
s = a′b+ab′ and
c = a.b
The logic circuit for the half adder is based on the Boolean expressions for the sum bit and the carry bit are given below –
(II) Full Adder
- This adder adds three single-bit binary numbers (a, b, and Carry-in [cin]).
- This adder results in two output forms – Sum (s) and Carry-out (cout).
Truth Table:
| a | b | cin | Sum (s) | Carry-out (cout) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Logic Equations:
- Sum (s) = a ⊕ b ⊕ cin
- Carry-out (cout) = (a ⋅ b) + (cin ⋅ (a ⊕ b))
Circuit Diagram:
Finally, the Boolean functions based on the above K-maps of the full adder are given below:
s = a′.b′.cin + a′.b.c’in + a.b.cin + a.b′.c’in
cout = a.b + b.cin + a.cin
Thus, the logic circuit for a full adder for the sum bit and the carry bit is –
(III) Ripple Carry Adder
- This adder is an advanced form of a Full adder.
- This adder adds multi-bit binary numbers by cascading full adders.
- It consists of N full adders for N-bit number addition.
- It gives Sum bits and a final Carry-out.
- The Carry-out value from each full adder is connected to the Carry-in of the next higher-order full adder.
- Demerits:
- It shows propagation delay, i.e., the time taken for the carry to propagate through all full adders, leading to slower addition as the number of bits increases.
(IV) Look-Ahead Carry Adders
- Look-ahead carry adders are an advanced form of Ripple Carry Adders, and other more complex adder architectures can be used to reduce propagation delay.
0 Comments